Objective Truth and Personal Faith

In choosing teaching as a career and mathematics as my discipline, the objectivity and certainty of solving equations or evaluating expressions appealed to me. To adapt a phrase from the 1970‘s that I expect will be familiar to my readers, “When Pythagoras talks, people listen!”¹ There was a satisfaction when the answer reached on my homework matched the answer in the last section of the Mathematics textbook. This same math put astronauts on the moon and allowed the bank customer to reconcile her accounts with the monthly bank statement. What chaos would ensue if a set of addition and subtraction problems was prone to two (or even worse several) answers!

Author George Orwell in his dystopian novel 1984 introduced his readers to the idea that government propagandists will force “2+2=5” as a (changeable) fact on its citizens. Orwell in an earlier review of a Bertrand Russell piece wrote, “We have now sunk to a depth at which the restatement of the obvious is the first duty of intelligent men.”² I have wondered if Orwell‘s math was the inspiration for a Star Trek: The Next Generation episode during which Captain Picard‘s Cardassian³ captor insisted he state he saw five lights when both he and the television audience could clearly see there were only four lights.⁴

Truth, belief, propaganda, post-truth – what to make of it all? My naïve sense that mathematics bore an immunity to these nuances and deceptions now requires new scrutiny in light of a publication titled, A Pathway To Equitable Math Instruction⁵ which states, “We see white supremacy culture show up in the mathematics classroom even as we carry out our professional responsibilities.” In support of this premise, the article cites traditional mathematical protocols like:

• The focus is on getting the “right” answer
• Teachers are teachers and students are learners
• State standards guide learning in the classroom
• “I do, we do, you do” is the format of the class
• Students are required to “show their work”

The foregoing is not intended to be a review of the document but a quick glance at the list may reveal three symptoms: “think our way, do as we say, do it our way.” Adherents to Critical Theory⁶ push back against this hierarchical social structure and consider these three symptoms as a result of a system of oppression and control. The motivation for this article is neither a defense of mathematics nor a defense of mathematical education. I will leave it at this – it is an enormous leap from teaching how to solve a quadratic equation to government oppression throughout the world. I always thought I was changing the world for the better – both individually for my students and collectively through their careers – rather than contributing to an antiquated and abhorrent system that needed to be abolished. For this article I hold in view for our consideration the first bulleted item above – the focus on getting the “right answer.” This quality of mathematics drew me in the first place and accomplishments great and mundane resulted from the right answer (and tragedy from the wrong one!)⁷

The student of quantum mechanics is quickly confronted with Heisenberg‘s uncertainty principle. “Introduced first in 1927 by the German physicist Werner Heisenberg, the uncertainty principle states that the more precisely the position of some particle is determined, the less precisely its momentum can be predicted from initial conditions, and vice versa.”⁸ The implications of this principle along with subsequent developments and discoveries far exceed this one sentence summary. I introduce it only to say that there is an element of uncertainty in mathematics and science. For extra credit, the Gracious Reader can search “stochastic mathematics” or “stochastic processes.”⁹

The remaining paragraphs in this article will introduce you to Thomas Bayes, the Bayes‘ Theorem and Bayesian Inference. There is insufficient space to fully develop any of these ideas and what follows is a short introduction.

Englishman Thomas Bayes was a Presbyterian minister and a prominent mathematician. He lived in the early- to mid-eighteenth century and the theorem which bears his name – Bayes‘ Theorem – remains relevant today. Bayes‘ Theorem is used in making decisions and predictions in a wide range of arenas¹⁰ including healthcare, cybersecurity and even the courtroom. One exciting application involves a search for John Aldridge who had fallen into the water from his boat off the shores of Long Island.¹¹ I hear you asking, “So what is Bayes‘ Theorem and what calculator has a ‘BT‘ button on it?”

There will be no deep dive into the calculations and computations using Bayes‘ Theorem; instead, this article introduces the epistemological implications of this theorem. For those of you interested, here is one version of Bayes‘ Theorem.

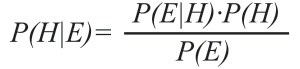
Where H stands for “hypothesis” and E stands for “evidence”

In Bayesian inference, probability is thought of as a measure of the strength of belief in the hypothesis. The following description applies to the book titled Bayesian Epistemology co-authored by Luc Bovens and Stephan Hartmann. “Probability theory is increasingly important to philosophy. Bayesian probabilistic models offer us ways of getting to grips with fundamental problems about information, coherence, reliability, confirmation, and testimony, and thus show how we can justify beliefs and evaluate theories. Bovens and Hartmann provide a systematic guide to the use of probabilistic methods not just in epistemology, but also in philosophy of science, voting theory, jurisprudence, and cognitive psychology.”¹²

Avoiding math jargon and long calculations, P(H) (read “P of H”) represents the strength of one‘s belief in a given hypothesis. A probability of zero “0” means the hypothesis is impossible and therefore false. A probability of one “1” means the hypothesis is certain and therefore true. Probabilities expressed as a proper fraction or as a decimal measure the level of certainty or confidence one has in the hypothesis. A value near one (say 0.95 or 10/11) is very persuasive with a high level of certainty. A value near zero is unpersuasive and doubtful. That is intuitive enough once the terminology becomes familiar.

While P(H) represents the prior probability or belief, P(H|E) (read “P of H given E”) represents the posterior probability or belief when some piece of new evidence E is introduced. New information should influence current ideology, either confirming a hypothesis thereby increasing the likelihood of its truth or resisting it thereby decreasing the likelihood of its truth. Our prior belief becomes more or less likely given new evidence. Today‘s posterior belief becomes tomorrow‘s prior belief in what is a never-ending cycle of learning, processing, confirming or adjusting our doctrine and dogma.

Consider the question of the location of the Temple in Jerusalem.¹³ If there are five scholars in a room, each should be able to agree that there must be a physical location – an actual plot of land – on which the Temple rested. Each can hold a different view as to the location of this plot of land - I have identified five (5) possible and popular sites that are currently under consideration. Imagine each of our scholars holds a different view based on an analysis of the available evidence. As new evidence is discovered and vetted, this should influence each position and either promote it or resist it. There is no anger or argument in this process – leave it to Bayes and other mathematicians to find a civil (if dry and nerdy) way to settle a dispute!

This is part of an ongoing series to be persuasive in today‘s interactions. And while doing calculations will not win the argument, understanding the fundamental issues underlying Bayes‘ may be helpful. This article pairs with last month‘s article recommending an ask be made of the doubter. Too often we consider debate as a win / loss effort and Bayes suggests it is a process of moving closer to certainty or closer to impossibility. “Then Agrippa said to Paul, “You almost persuade me to become a Christian.””¹⁴ “I call to remembrance the genuine faith that is in you, which dwelt first in your grandmother Lois and your mother Eunice, and I am persuaded is in you also.”¹⁵ With a goal of persuasion rather than victory, we may be more effective in showing people “the Way, the Truth and the Life.”¹⁶